Càlcul de la força del premsablanques: Atureu les arrugues abans que arruïnin el vostre embutit

Comprendre els fonaments de la força del portamatriu

Ha vist alguna vegada com una xapa metàl·lica perfectament bona s'arruga fins a convertir-se en ones inutilitzables durant una estampació profunda? Aquest resultat frustrant sovint es deu a un factor clau: la força del portamatriu. Aquest paràmetre fonamental determina si la seva operació de conformació produeix peces i closques impecables o rebuts destinats a la brossa de reciclatge.

La força del portamatriu (BHF) és la pressió de fixació aplicada a la zona de brida d'una xapa metàl·lica durant operacions d'estampació profunda. Penseu-hi com una agafada controlada que guia el flux de material des de la brida cap a la cavitat de la matriu. Quan s'aplica la quantitat adequada de força, la xapa llisca uniformement sobre el radi de la matriu, formant una paret amb gruix uniforme sense defectes. Si l'ajuste és incorrecte, entendreu ràpidament per què dominar el càlcul de la força del portamatriu és tan important en la conformació precisa de metalls.

Què controla la força del portablanques en l'estampació profunda

La física darrere de la força del portablanques està directament relacionada amb el comportament del metall sota tensió. A mesura que el punçón baixa i estira el material cap al motlle, la brida experimenta tensions compressives en direcció circumferencial. Sense una restricció adequada, aquestes tensions provoquen arrugues i pandeig a la brida. El portablanques proporciona aquesta restricció essencial mitjançant l'aplicació de pressió perpendicular a la superfície de la xapa.

El càlcul adequat de la força del portablanques proporciona tres resultats principals:

• Flux de material controlat :La força regula la rapidesa i uniformitat amb què la xapa entra a la cavitat del motlle, evitant la formació de parets irregulars
• Prevenció de les arrugues: Una pressió adequada suprimeix el pandeig per compressió a la zona de la brida on les tensions circumferencials són més elevades
• Evitació de l'afinament excessiu: Mitjançant l'equilibri entre fricció i flux, una força adequada del portablanques evita l'estirament localitzat que condueix a fractures a la paret

Aquests resultats depenen en gran mesura de comprendre la relació entre el límit d'elasticitat, la tensió d'elasticitat i les característiques del límit d'elasticitat del vostre material específic. La força d'elasticitat necessària per iniciar la deformació plàstica estableix la base per a quant pressió heu de controlar el comportament del material durant l'estirat.

L'equilibri entre arrugament i ruptura

Imagineu-vos caminant sobre una corda fluixa entre dos modes de fallada. D'un costat, una força d'adherència insuficient (BHF) permet que la brida s'arrugi quan les tensions compressives superen la resistència al vinclament del material. De l'altre costat, una força excessiva crea una fricció tan elevada que la paret s'estira més enllà dels seus límits de conformació, provocant esquinçaments o fractures properes al radi del punxó.

Quan la força de subjectació del blanque (BHF) és massa baixa, notareu rebaixos ondulats i parets arrugades que fan que les peces no siguin dimensionalment acceptables. El material pràcticament pren el camí de mínima resistència, arrugant-se cap amunt en lloc d'fluir suaument cap a la matriu. Això difereix significativament d'operacions com el tall cònic, on la retirada controlada del material segueix camins previsibles.

Quan la força de subjectació del blanque (BHF) és massa alta, la fricció excessiva impedeix un flux adequat del material. El punçó continua la seva cursa, però el rebaix no pot alimentar prou ràpid per subministrar la paret. Això crea un aprimament perillós, normalment al radi del punçó on les concentracions d'esforç són més elevades. A diferència de les operacions de tall cònic que retiren el material progressivament, el conformant profund redistribueix el material, i una restricció excessiva interromp aquesta redistribució de manera catastròfica.

La finestra òptima de BHF depèn de diversos factors interconnectats: la relació d'estampat (la relació entre el diàmetre de la planxa i el diàmetre del punzó), el gruix del material i la resistència a la fluència específica del vostre material en fulla. Una relació d'estampat més elevada exigeix un control de força més precís perquè l'àrea de la brida és més gran i les tensions compressives són més significatives. Els materials més fins requereixen forces proporcionals més baixes però són més sensibles a les variacions.

Per als enginyers i dissenyadors d'utillatges, comprendre aquests fonaments proporciona la base per a càlculs precisos. Heu d'entendre per què la força és important abans de poder determinar-ne la quantitat a aplicar. Les seccions següents desenvoluparan aquests conceptes, transformant la física en fórmules pràctiques i metodologies reals que produeixen peces consistents i lliures de defectes.

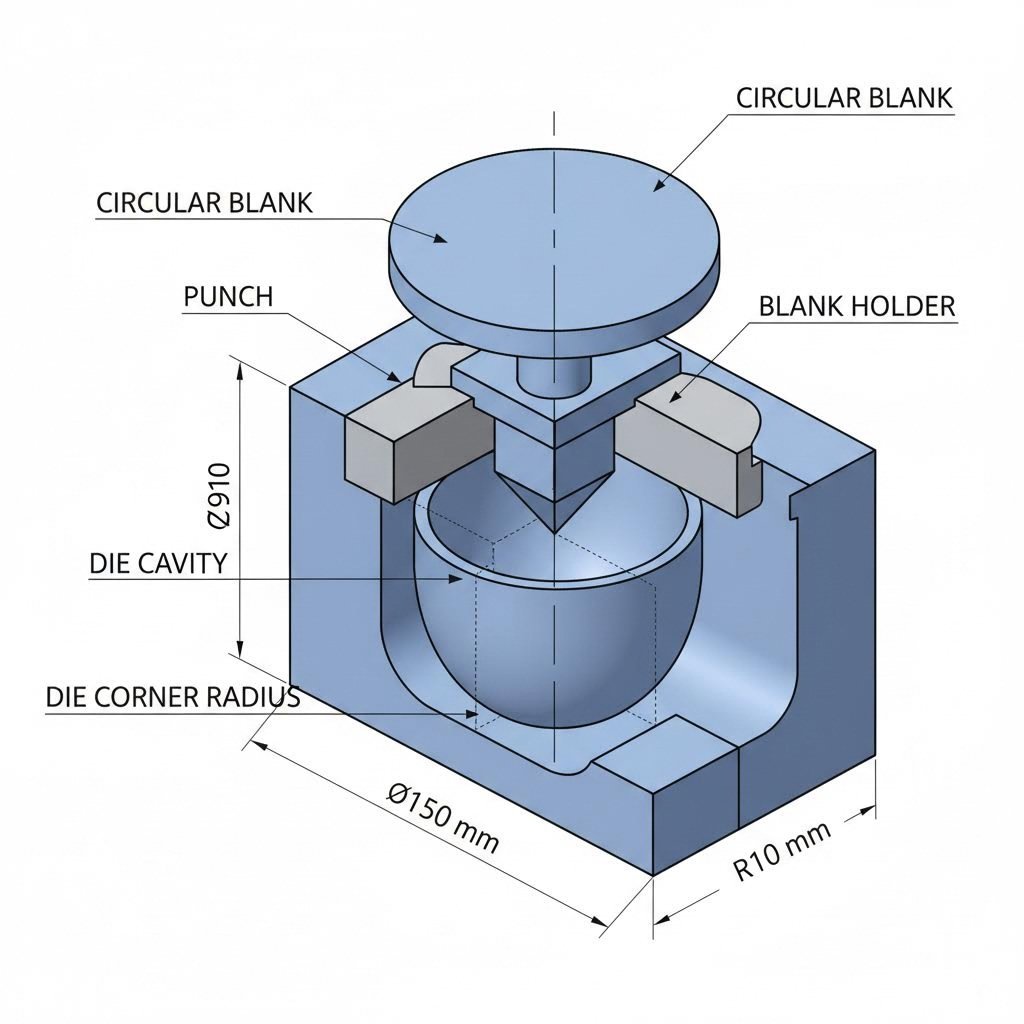
Fórmules bàsiques per al càlcul de la força del portablanques

Ara que enteneu per què és important la força del portamotlles, traduïm aquests fonaments en xifres concretes. Les fórmules matemàtiques per al càlcul de la força del portamotlles tanquen la llacuna entre la comprensió teòrica i l'aplicació al taller. Aquestes equacions us proporcionen valors concrets per programar a la premsa o especificar en la documentació del vostre motlle.

La bellesa d’aquestes fórmules rau en la seva practicitat. Tenen en compte la geometria, les propietats del material i el mòdul d’elasticitat dels metalls que esteu conformant. Tant si esteu embutint copes d’acer suau com carcases d’aliatge d’alumini, s’aplica la mateixa equació fonamental amb ajustos específics segons el material.

Explicació de la fórmula estàndard de BHF

La fórmula principal per al càlcul de la força del portamotlles es basa en un concepte clau: cal disposar de prou pressió sobre la zona de brancada per evitar arrugues sense restringir el flux de material. Aquesta és l'equació estàndard:

BHF = π/4 × [(D₀² - (d + 2rd)²)] × p

Sembla complex? Descomponem-ho. Aquesta fórmula calcula la força total multiplicant l'àrea efectiva de la brida per la pressió específica del portamatriu necessària pel vostre material. El resultat proporciona la força en newtons quan s'utilitzen unitats SI consistents.

El terme π/4 × [(D₀² - (d + 2rd)²)] representa l'àrea anular de la brida que queda sota el portamatriu. Imagineu-vos un anell amb forma de rosquilla fet de material. El límit exterior és el diàmetre de la vostra xapa, i el límit interior és on el material passa a la cavitat de la matriu. Aquesta àrea disminueix a mesura que avança l'estirat, raó per la qual algunes operacions es beneficien del control de força variable.

Descomposició de cada variable

Comprendre cada variable us ajuda a aplicar correctament la fórmula i solucionar problemes quan els resultats no coincideixen amb les expectatives:

• D₀ (Diàmetre de la xapa): El diàmetre inicial de la vostra xapa circular abans de formar-la. Aquest valor prové directament dels vostres càlculs de desenvolupament de la xapa basats en la geometria de la peça acabada.
• d (Diàmetre del punzó): El diàmetre exterior del vostre punçó, que determina el diàmetre interior de la vostra copa estirada. Aquest valor és típicament un paràmetre de disseny fix.
• rd (Radi de cantell de matriu): El radi a l'entrada de la matriu on el material es doblega i flueix cap a la cavitat. Un radi més gran redueix la força d'estirat però augmenta lleugerament la superfície efectiva de la brida.
• p (Pressió específica del retenidor de xapa): La pressió per unitat d'àrea aplicada a la brida, expressada en MPa. Aquesta variable requereix una selecció cuidadosa segons les propietats del material.

El valor de pressió específica p meréixer atenció especial perquè està directament relacionat amb les característiques del límit elàstic o tensió de fluència del vostre material. Els materials amb un límit elàstic més alt en aplicacions tècniques requereixen proporcionalment pressions específiques més altes per mantenir un control adequat durant el formant.

Valors recomanats de pressió específica segons el material

Seleccionar la pressió específica adequada és on la ciència dels materials es troba amb la conformació pràctica. El mòdul de tracció que presenta l'acer difereix significativament de les aliatges d'alumini o coure, i aquestes diferències influeixen en la manera com cal restringir agressivament la brida. El mòdul d'elasticitat de l'acer també afecta el comportament del retroces, tot i que la seva influència principal sobre la força de sujecció (BHF) prové de la relació amb la resistència a la fluència.

Material	Pressió específica (p)	Interval típic de resistència a la fluència	Notes
Acer dolç	2-3 MPa	200-300 MPa	Comenceu per l'extrem inferior per a gruixos més petits
Acer inoxidable	3-4 MPa	200-450 MPa	Una major endurement per deformació requereix l'interval superior
Aliatges d'alumini	1-2 MPa	100-300 MPa	Sensible a les condicions de lubricació
Aliatges de coure	1,5-2,5 MPa	70-400 MPa	Varia significativament segons la composició de l'aliatge

Fixeu-vos com la pressió específica es correlaciona amb els intervals de resistència a la fluència. Materials d'alta resistència generalment necessiten pressions de manteniment més elevades perquè oposen més resistència a la deformació. Quan treballeu amb un material al límit superior del seu interval de resistència, seleccioneu pressions properes als valors recomanats més alts.

Aproximacions empíriques versus analítiques

Quan us hauríeu de basar en la fórmula estàndard i quan necessiteu mètodes més sofisticats? La resposta depèn de la complexitat de la peça i dels vostres requisits de producció.

Utilitzeu fórmules empíriques quan:

• Dibuixeu formes simples axialment simètriques com peces cilíndriques
• Treballant amb materials ben caracteritzats i processos establerts
• Els volums de producció justifiquen l'optimització basada en prova i error
• Les toleràncies de les peces permeten certa variació en el gruix de la paret

Considereu enfocaments analítics o basats en simulacions quan:

• Formeu geometries complexes no axialment simètriques
• Dibuixeu materials d'altes prestacions o exòtics amb dades limitades
• Les toleràncies ajustades exigeixen un control precís
• Els volums de producció no permeten iteracions extenses d'intent

La fórmula estàndard proporciona un excel·lent punt de partida per a la majoria d'aplicacions. Normalment assolireu una precisió del 80-90% en els càlculs inicials, i després podreu ajustar segons els resultats de les proves. Per a aplicacions crítiques o materials nous, combinar els valors calculats amb validació mitjançant simulació redueix significativament el temps de desenvolupament i les taxes de rebuig.

Amb aquestes fórmules a mà, esteu preparats per calcular els valors teòrics de BHF. Tanmateix, en l'estampació real intervé la fricció entre les superfícies de l'eina i la vostra xapa, i aquests efectes de fricció poden alterar significativament els vostres resultats.

Coeficients de fricció i efectes de la lubricació

Heu calculat la vostra força del premsaplomes utilitzant la fórmula estàndard, introduït tots els valors correctes i el número sembla bo sobre el paper. Però quan executeu les primeres peces, alguna cosa no funciona. El material no flueix com esperàveu o observeu ratllades a la superfície que no estaven previstes. Què ha passat? La resposta sovint es troba en la fricció, la variable invisible que pot fer o trencar el vostre càlcul de força del premsaplomes.

La fricció entre les superfícies de la xapa, la matriu i el premsaplomes influeix directament en la quantitat de força que realment limita el flux del material. Ignoreu-la, i la vostra força del premsaplomes calculada amb cura es converteix en poc més que una suposició raonada. Compteu-ne adequadament, i obtindreu un control precís sobre el vostre procés d'embutició.

Com canvia la fricció els vostres càlculs

La relació entre la fricció i la força del premsatxes segueix un principi senzill: una fricció més elevada amplifica l'efecte de restricció de qualsevol força donada. Quan el coeficient de fricció augmenta, la mateixa força del premsatxes produeix una resistència major al flux del material. Això vol dir que la força calculada pot ser massa agressiva si la fricció és superior a la suposada, o massa dèbil si la lubricació redueix la fricció per sota dels nivells esperats.

La fórmula modificada que té en compte la fricció relaciona tres paràmetres clau:

Força d'embutició = BHF × μ × e^(μθ)

Aquí, μ representa el coeficient de fricció entre les superfícies en contacte, i θ és l'angle d'envolvent en radians on el material contacta amb el radi de la matriu. El terme exponencial reflecteix com la fricció s'acumula a mesura que el material envolta superfícies corbes. Fins i tot canvis petits en μ provoquen diferències significatives en la força necessària per embutir el material a la cavitat de la matriu.

Penseu què passa quan dupliqueu el coeficient de fricció de 0,05 a 0,10. La força d'estirat no es duplica simplement. Al contrari, la relació exponencial significa que la força augmenta de manera més pronunciada, especialment en geometries amb angles d'envoltura més grans. Això explica per què la selecció del lubricant és tan important com el vostre càlcul inicial de BHF.

Els coeficients de fricció típics varien àmpliament segons les condicions de la superfície i els lubricants:

• Acer sec sobre acer: 0,15-0,20 (rarament acceptable per a formació en producció)
• Lubricació amb oli lleuger: 0,10-0,12 (adequat per a estirats superficials i materials de baixa resistència)
• Compostos d'estirat pesats: 0,05-0,08 (estàndard per a estirats moderats o profunds)
• Pel·lícules polimèriques: 0,03-0,05 (òptim per a aplicacions exigents i materials d'alta resistència)

Aquests intervals representen punts de partida. Els coeficients reals depenen de la rugositat de la superfície, la temperatura, la velocitat d'estirat i la consistència de l'aplicació del lubricant. Quan el vostre BHF calculat produeix resultats inesperats, la variació del coeficient de fricció sovint n'és la causa.

Estratègies de lubricació per a un flux òptim del material

La selecció del lubricant adequat implica ajustar les característiques de fricció als requisits del formatge. Una fricció més baixa permet que el material flueixi més lliurement, reduint el BHF necessari per evitar esquinçaments. Tanmateix, una fricció excessivament baixa pot requerir un BHF més alt per prevenir arrugues, ja que el material ofereix menys resistència natural al vinclament.

Els materials galvanitzats per immersió en calent presenten reptes únics que il·lustren aquest equilibri. El recobriment de zinc en l'acer galvanitzat per immersió en calent crea característiques de fricció diferents comparades amb l'acer nu. La capa més tova de zinc pot actuar com un lubricant integrat sota pressions lleugeres, però també es transfereix a les superfícies dels motlles durant llargs cicles de producció. Aquest comportament del recobriment de zinc galvanitzat per immersió en calent significa que el coeficient de fricció pot variar durant un cicle de producció, requerint ajustos en la força d'agafatge del marc o un manteniment més freqüent del motlle.

Quan es formen materials galvanitzats, molts enginyers comencen amb pressions específiques més baixes i les van augmentant gradualment durant els assaigs. L'efecte lubricant del recobriment de zinc sovint implica que es necessita un 10-15% menys de força d'agafatge del marc comparat amb acer sense recobrir del mateix grau. Tanmateix, les variacions en el gruix del recobriment entre proveïdors poden afectar la consistència, fet que fa essencial la documentació i la verificació del material entrant.

Com afecta l'enduriment per deformació als requisits de fricció

Aquí és on la conformació es torna interessant. A mesura que progressa la passada d'estirat, el material no és el mateix metall que quan es va començar. Els fenòmens d'enduriment per deformació i d'enduriment mecànic transformen les propietats del material en temps real, i aquests canvis afecten el comportament del fregament durant tota l'operació.

Durant l'estirat profund, el material de la brida pateix una deformació plàstica abans d'entrar a la cavitat de la matriu. Aquest enduriment per deformació augmenta localment la resistència a la fluència del material, fins i tot en un 20-50% segons l'aliatge i el nivell de deformació. L'enduriment mecànic fa que el material sigui més rígid i més resistent a deformacions addicionals, cosa que canvia com interactua amb les superfícies de la matriu.

Què significa això per la fricció? Un material més dur i treballat genera característiques de fricció diferents que el material inicial més tou. Les asperitats superficials es comporten de manera diferent, les pel·lícules lubricants poden fer-se més fines sota pressions de contacte més elevades, i el coeficient de fricció global pot augmentar a mesura que avança l'estirat. Aquest procés d'enduriment per deformació i treball explica per què una força d'embolcall constant (BHF) a vegades produeix resultats inconstants, especialment en estirats profunds on es produeix una transformació significativa del material.

Les implicacions pràctiques inclouen:

• Les pel·lícules lubricants han de suportar pressions de contacte creixents a mesura que el material s'endureix
• L'acabat superficial de les motlles esdevé més crític al final de la correguda, quan la fricció tendeix a augmentar
• Els sistemes BHF variables poden compensar els canvis de fricció ajustant la força al llarg de tota la correguda
• Els materials amb taxes d'enduriment per treball elevades poden beneficiar-se d'estratègies de lubricació més agressives

Entendre aquesta relació dinàmica entre la transformació del material i la fricció ajuda a explicar per què els tècnics d'estampació experimentats sovint ajusten la força del premsatex segons factors que no apareixen en les fórmules estàndard. Estan compensant els efectes de fricció que canvien durant cada cicle d'estampació.

Ara que els efectes de la fricció formen part de la vostra eina de càlcul, esteu preparats per reunir-ho tot en un exemple complet desenvolupat amb números i unitats reals.

Metodologia de Càlcul Pas a Pas

Preparats per posar la teoria en pràctica? Recorrem junts un càlcul complet de la força del premsatex des del principi fins al final, utilitzant números reals que podrieu trobar a la planta de producció. Aquest exemple desenvolupat mostra exactament com s'uneixen tots els components de la fórmula, oferint-vos una plantilla que podeu adaptar a les vostres pròpies aplicacions.

La millor manera de dominar aquests càlculs és treballant amb un escenari real. Calcularem la BHF per a una operació comuna d'estampació profunda: formar una copa cilíndrica a partir d'un tovalló circular. Al llarg del procés, veuràs com les propietats del material, com la tensió de fluència de l'acer, influeixen en les teves decisions i com cada pas contribueix al valor final de la força.

Guia pas a pas del càlcul

Abans de començar amb els números, establim un enfocament sistemàtic. Seguir aquests passos en ordre assegura que no et perdis cap factor clau que afecti la precisió. Aquest mètode funciona tant si estàs calculant la força per a graus d'acer suau com per a aliatges d'alta resistència.

1. Determinar les dimensions del tovalló i el punxó: Recopila tots els paràmetres geomètrics, incloent el diàmetre del tovalló (D₀), el diàmetre del punxó (d) i el radi de la cantonada de la matriu (rd). Aquests valors normalment provenen dels plànols de la peça i de les especificacions del disseny de la matriu.
2. Calcular l'àrea de la brida sota el portamatriu: Apliqueu la fórmula de l'àrea anular per trobar la superfície sobre la qual actua la pressió del portablanques. Aquesta àrea determina quina força total resulta de la pressió específica seleccionada.
3. Seleccioneu una pressió específica adequada segons el material: Consulteu les taules de propietats dels materials per triar el coeficient de pressió correcte (p). Considereu la resistència a la fluència de l'acer o d'altres materials, el gruix i les condicions de la superfície.
4. Apliqueu la fórmula amb conversions d'unitats: Inseriu tots els valors a l'equació de BHF, assegurant unitats consistents en tot el procés. Convertiu els resultats finals a unitats pràctiques com ara quilonewtons per a la programació de la premsa.
5. Verifiqueu respecte als límits de la relació d'estirat: Comproveu que la vostra geometria es trobi dins dels límits acceptables de la relació d'estirat pel material i que la força calculada coincideixi amb les capacitats de l'equipament.

Exemple resolt amb valors reals

Calculem la força del portablanques per a un escenari pràctic que representa condicions típiques de producció.

Paràmetres donats:

• Diàmetre del buit (D₀): 150 mm
• Diàmetre del punçó (d): 80 mm
• Radi de la cantonada de la matriu (rd): 8 mm
• Material: Acer suau, gruix de 1,2 mm
• Tensió de fluència: aproximadament 250 MPa (típica per a grades comuns d'acer)

Pas 1: Confirmeu les dimensions

Primer, verifiqueu la vostra relació d'estirat per assegurar-vos que l'operació és factible. La relació d'estirat (β) equival al diàmetre del buit dividit pel diàmetre del punçó:

β = D₀ / d = 150 / 80 = 1,875

Per a l'acer suau en una primera operació d'estirat, la relació d'estirat màxima recomanada sol oscil·lar entre 1,8 i 2,0. La nostra relació de 1,875 es troba dins dels límits acceptables, per tant podem continuar amb confiança.

Pas 2: Calculeu l'àrea de la brida

L'àrea de la brida sota el portablanques utilitza la fórmula de l'àrea anular. Necessitem el diàmetre interior efectiu, que té en compte el radi de la cantonada de la matriu:

Diàmetre interior efectiu = d + 2rd = 80 + 2(8) = 96 mm

Ara calculeu l'àrea anular:

A = π/4 × [(D₀)² - (d + 2rd)²]

A = π/4 × [(150)² - (96)²]

A = π/4 × [22,500 - 9,216]

A = π/4 × 13,284

A = 0,7854 × 13,284

A = 10.432 mm² (o aproximadament 104,32 cm²)

Pas 3: Seleccioneu la pressió específica

Per a l'acer suau amb una tensió de fluència en el rang de 200-300 MPa, la pressió específica recomanada oscil·la entre 2-3 MPa. Atès el nostre gruix de 1,2 mm (no extremadament fi) i la resistència típica a la fluència d'aquest tipus d'acer, seleccionarem:

p = 2,5 MPa (el centre del rang recomanat)

Aquesta selecció té en compte les condicions típiques de lubricació i proporciona un marge contra arrugaments i ruptures.

Pas 4: Apliqueu la fórmula

Ara combinem l'àrea i la pressió per trobar la força total:

BHF = A × p

BHF = 10.432 mm² × 2,5 MPa

Com que 1 MPa = 1 N/mm², el càlcul queda com:

BHF = 10,432 mm² × 2,5 N/mm²

BHF = 26.080 N

BHF = 26,08 kN

Pas 5: Verificació respecte als límits

Amb la força calculada d'aproximadament 26 kN, hem de confirmar que aquest valor és raonable per al nostre equip i disseny de matriu.

Sempre heu de comparar la vostra força BHF calculada amb dos límits crítics: la capacitat màxima del subjectador de premsa i les especificacions de disseny de la matriu. La vostra força calculada ha de ser inferior a la capacitat de la premsa i, alhora, superior al llindar mínim necessari per evitar arrugues. En aquest exemple, una premsa amb una capacitat de subjectador de 50+ kN ofereix un marge adequat, i els 26 kN calculats haurien de controlar eficacement el flux de material per a la nostra geometria i tipus d'acer.

Interpretació dels resultats

Els 26 kN representen el punt de partida per a la prova. En la pràctica, podreu ajustar aquest valor en un ±10-15% segons el comportament real del material i l'efectivitat de la lubricació. Així és com s'interpreta el càlcul:

Paràmetre	Valor calculat	Consideració pràctica
Àrea de brida	10.432 mm²	Disminueix a mesura que avança l'embutició
Pressió específica	2,5 MPa	Ajusteu segons els resultats reals de límit elàstic
Força total de pinçament (BHF)	26,08 kN	Valor inicial per a la configuració de la premsa
Relació d'embuts	1.875	Dins dels límits segurs per a una sola embutició

Si les primeres peces d'assaig presenten lleus arrugues, augmenteu la pressió fins a 2,8-3,0 MPa. Si observeu reducció de gruix propera al radi del punxó o signes d'inici de ruptura, reduïu-la fins a 2,0-2,2 MPa. El càlcul proporciona una base científica, però l'optimització final requereix observar el comportament real del material.

Fixeu-vos en com la tensió de fluència del grau d'acer específic ha influït en la nostra selecció de pressió. Els graus d'acer més resistents us portarien cap a l'extrem superior de l'interval de pressió, mentre que els acers més tous per embutició podrien permetre valors més baixos. Sempre verifiqueu que les certificacions del material coincideixin amb les vostres suposicions abans de les tirades de producció.

Amb un valor calculat fiable a mà, podeu perfeccionar encara més el vostre enfocament comprenent com els diagrames de límit d'embolcallament revelen els límits entre l'embolcallament exitós i els modes de fallada.

Diagrames de Límit d'Embolcallament i Optimització de Força

Heu calculat la vostra força del premsafulles i fins i tot heu tingut en compte els efectes de fricció. Però com sabeu si aquest valor calculat produirà realment peces bones? Aquí és on els diagrames de límit d'embolcallament es converteixen en la vostra eina de validació. Un diagrama de límit de conformabilitat marca el límit entre l'embolcallament exitós i la fallada, donant-vos una confirmació visual que els vostres ajustos de força del premsafulles mantenen l'operació en una zona segura.

Penseu en un FLD com en un mapa del camí per al vostre material. Mostra exactament quant d'esforç pot suportar la xapa abans que passi alguna cosa errada. Entenent on cau la vostra operació d'embutició en aquest diagrama, podeu predir si el càlcul de la força del premsablanques produirà peces lliures de arrugues i trencaments abans de posar en marxa el primer blanquet.

Lectura de diagrames de límit d'embuts per a l'optimització de la força del premsablanques

Un diagrama de límit d'embuts representa l'esforç major (la deformació principal més gran) a l'eix vertical contra l'esforç menor (la deformació perpendicular a l'esforç major) a l'eix horitzontal. La corba resultant, sovint anomenada corba de límit d'embuts (FLC), representa el llindar on comença la fallada del material. Qualsevol combinació d'esforços per sota d'aquesta corba és segura; qualsevol cosa per sobre comporta risc de collaret, esquinçament o fractura.

Quan examineu un FLD, notareu que no és simètric. La corba normalment baixa fins al mínim a prop del centre, on la deformació menor és zero (condició de deformació plana), i puja per ambdós costats. Aquesta forma reflecteix com el material es comporta de manera diferent sota diversos estats de deformació. L'estirament biaxial al costat dret del diagrama i l'estampació/compressió al costat esquerre tenen límits de ruptura diferents.

Comprendre les zones clau d'un FLD us ajuda a interpretar on cau la vostra operació:

• Regió segura d'embutició: Combinacions de deformació clarament per sota de la FLC on el material flueix sense risc de fallada. Aquesta és la vostra zona objectiu per a una producció fiable.
• Zona marginal: L'àrea just per sota de la FLC on les peces poden superar la inspecció però tenen un marge de seguretat reduït. Variacions del material o desviacions del procés podrien provocar fallades.
• Zona d'estricte/ruptura: Combinacions de deformació a nivell de la FLC o per sobre d'aquesta on l'afinament localitzat condueix a fissures i esquinçaments. Les peces formades aquí no superaran els controls de qualitat.
• Zona d'arrugament: La regió inferior esquerra on les deformacions compressives menors excessives provoquen arrugament. Això indica una força del premsatelles insuficient per controlar el flux del material.

La relació entre la resistència a la tracció i la límit d’elasticitat afecta on es situa la corba de límits de conformabilitat (FLC) del vostre material. Els materials amb major allargament abans de l’estricció solen tenir corbes FLC situades més amunt al diagrama, oferint finestres de conformabilitat més grans. En canvi, els materials d’alta resistència amb menor allargament tenen les corbes FLC més properes a l’origen, requerint un control més precís de la força del premsatelles (BHF).

Relacionar les dades de FLD amb els ajustos de força

Aquí és on el diagrama de límits de conformabilitat (FLD) esdevé pràctic per a l'optimització de la força del premsatelles. La vostra força del premsatelles influeix directament en el camí de deformació que segueix el material durant el formatejat. Si augmenteu la força, desplaceu el camí de deformació cap a un estirat biaxial més pronunciat (cap a la dreta al diagrama). Si reduïu la força, el camí es desplaça cap a condicions d’estampat (cap a l’esquerra, cap a possibles arrugaments).

Imagineu que el vostre BHF actual produeix una trajectòria de deformació que passa perillosament a prop de la zona d'arrugament. El FLD us indica immediatament: augmenteu la força calculada per desplaçar la trajectòria cap amunt i cap la dreta, allunyant-vos de la fallada per compressió. Al contrari, si les mesures de deformació mostren que s'apropa al límit d'estricció, reduir el BHF permet un flux de material més gran, desplaçant la trajectòria lluny de la corba de fallada.

Els materials diferents requereixen enfocaments fonamentalment diferents perquè els seus FLD varien significativament:

• Acer suau: Normalment ofereix finestres d'estampació generoses amb FLC situades relativament altes. Els càlculs estàndard de BHF funcionen bé, amb un rang d'ajust moderat durant la prova.
• Aliatges d'alumini: Generalment tenen FLC més baixos en comparació amb l'acer d'espessor similar, exigint un control més estricte del BHF. El mòdul d'elasticitat de l'alumini també influeix en el comportament del retorn elàstic, afectant les dimensions finals de la peça encara que la conformació sigui exitosa.
• Acero inoxidable: Unes taxes elevades d'enduriment per deformació desplacen la LFC durant el conformat, cosa que significa que els camins de deformació han de tenir en compte la transformació del material. Sovint cal ajustar les configuracions inicials de la força del premsablanques a mesura que s’acumulen dades de producció.

En el cas especial dels aliatges d'alumini, el mòdul d'elasticitat més baix de l'alumini en comparació amb l'acer fa que aquests materials es deflecteixin més sota càrregues determinades. Això afecta com es distribueix la pressió del premsablanques al llarg de la brida i pot crear concentracions de deformació localitzades si la distribució de pressió no és uniforme.

Per utilitzar eficaçment les dades de LFD en el vostre procés de treball, mesureu les deformacions en peces experimentals mitjançant anàlisi de quadrícula circular o correlació d'imatges digitals. Representeu gràficament aquestes deformacions mesurades sobre la LFD del vostre material. Si els punts s'agrupen prop de la zona d'arrugament, augmenteu la força del premsablanques. Si els punts s'acosten a la LFC, reduïu la força o millorreu la lubricació. Aquesta validació iterativa converteix la vostra força del premsablanques calculada, d’un valor teòric, en un ajust provat en producció.

La connexió entre l'anàlisi del diagrama de límits de conformació (FLD) i el càlcul de la força del premsaplomes uneix dues disciplines que molts enginyers tracten per separat. La vostra fórmula us proporciona un valor inicial; el FLD confirma si aquest valor funciona realment per a la vostra geometria i combinació de materials concretes. Quan aquestes eines treballen conjuntament, s'aconsegueixen taxes d'èxit en el primer intent que els mètodes d'assaig i error simplement no poden igualar.

Encara que la validació mitjançant FLD funcioni bé per a sistemes de força constant, algunes aplicacions es beneficien de l'ajust de la força al llarg de tota la cursa d'estampació. Els sistemes de força variable del premsaplomes ofereixen aquesta capacitat, obrint noves possibilitats per a geometries complexes.

Sistemes de Força Variable del Premsaplomes

I si la vostra força de premsatelles pogués adaptar-se en temps real mentre el punçó baixa? En lloc d'aplicar una pressió fixa durant tota la cursa, imagineu-vos un sistema que comenci amb una força més elevada per evitar les arrugues inicials i després reduir gradualment la pressió a mesura que l'àrea de brida disminueix. Això no és ciència ficció. Els sistemes de força variable del premsatelles (VBF) ofereixen exactament aquesta capacitat, i estan transformant la manera en què els fabricants aborden operacions complexes d'estampació profunda.

La força constant del premsatelles funciona bé per a geometries senzilles i materials tolerants. Però quan esteu arribant al límit de les relacions d'estirat, treballant amb materials propensos al endureixement per deformació, o formant formes complexes on els camins de deformació varien dràsticament en diferents parts de la peça, un únic valor de força simplement no pot optimitzar totes les fases de l'estirat. Els sistemes VBF solucionen aquesta limitació tractant la força del premsatelles com una variable de procés dinàmica en lloc d'un paràmetre fix.

Quan la força variable supera la força constant

Considereu què passa realment durant un embutit profund. Al començament de la cursa, tota la zona de brida està sota el portamatriu, i les tensions compressives són màximes. És en aquest moment quan el risc d'arrugament és més elevat, requerint una força de retenció considerable. A mesura que el punzó continua descendent, el material flueix cap a la cavitat de la matriu, reduint progressivament la superfície de la brida. Al final de la cursa, només queda un petit anell de material sota el portamatriu.

Aquest és el problema de la força constant: la pressió que evita l'arrugament al començament de la cursa pot generar fricció excessiva i risc de ruptura a mesura que la brida es redueix. A la inversa, una força optimitzada per a les condicions finals de la cursa us fa vulnerables a l'arrugament inicial. Esteu obligats a arribar a un compromís, acceptant condicions subòptimes en algun moment de cada cicle.

Els sistemes VBF eliminen aquest compromís adaptant la força a les condicions instantànies. La càrrega de fluïdesa necessària per iniciar el flux plàstic en la brida canvia a mesura que el material s'endureix durant la conformació. Un perfil VBF correctament programat té en compte aquests canvis, mantenint una restricció òptima durant tota l'operació. Els materials amb altes taxes d'enduriment per deformació s'beneficien especialment d'aquest enfocament, ja que les seves propietats canvien significativament durant cada impacte.

Les operacions d'hidroconformació mostren els principis VBF en la seva forma més sofisticada. En l'hidroconformació, la pressió del fluid substitueix el punçó rígid, i cal controlar amb precisió els perfils de pressió per assolir un flux uniforme del material. Aquests sistemes varien habitualment la pressió en un 50% o més durant un sol cicle de conformació, demostrant que el control dinàmic de la força permet obtenir geometries impossibles mitjançant aproximacions de pressió constant. Les lliçons extretes de l'hidroconformació s'apliquen directament al repussat convencional amb portablanques mecànics.

La conformació per rotació representa una altra aplicació on la força variable resulta essencial. A mesura que l'eina de rotació va modelant progressivament el material sobre un motlle, la força de retenció òptima canvia contínuament. Els enginyers que treballen en la conformació per rotació fa temps que saben que els ajustos de força estàtics limiten el que es pot aconseguir.

Tecnologies modernes de control de força variable

L'implementació d'una força variable del premsatelles requereix equipament capaç de modular la força amb precisió i repetibilitat. Els sistemes moderns de VBF solen utilitzar un dels tres enfocaments següents: coixinets hidràulics amb control servo, coixinets de matriu de nitrogen amb pressió ajustable o sistemes mecànics programables amb perfils de força accionats per came.

Els sistemes servo-hidràulics ofereixen la màxima flexibilitat. Els controladors programables ajusten la pressió d'oli als cilindres del portamotlles segons la posició del punzó, el temps o senyals de retroalimentació de força. Es pot crear pràcticament qualsevol perfil de força que permeti la física, i després desar i recuperar programes per a diferents peces. La configuració implica programar el perfil, produir peces de prova i refinar-lo segons els resultats.

Els sistemes basats en nitrogen proporcionen una implementació més senzilla a un cost inferior. Cilindres de nitrogen pressuritzat generen la força de subjecció, i reguladors ajustables o cilindres multietapa permeten certa variació de força durant la cursa. Tot i ser menys flexibles que els sistemes servo-hidràulics, els sistemes de nitrogen gestionen adequadament moltes aplicacions amb força variable.

Criteris	Força de subjecció constant	Força de subjecció variable
Adecuació a la complexitat de la peça	Formes simples axials simètriques, embuticions poc profundes	Geometries complexes, embuticions profundes, peces asimètriques
Requisits d'equipament	Prensa estàndard amb coixinet bàsic	Sistema de coixinet servo-hidràulic o programable
Temps de Preparació	Configuració inicial més ràpida, valor de força únic	Desenvolupament més llarg, però producció més repetible
Consistència de qualitat	Acceptable per a peces senzilles	Superior per a aplicacions complexes
Inversió de capital	Cost inicial més baix	Inversió inicial més elevada, sovint justificada pels guanys de qualitat
Aprofitament del material	Es requereixen mides estàndard de buits	Potencial per a buits més petits degut a un millor control del flux

Selecció entre enfocaments constants i variables

No totes les aplicacions justifiquen la complexitat del VBF. Fer la tria adequada requereix avaluar diversos factors de manera sistemàtica.

Geometria de la peça impulsa l'avaluació inicial. Les embuticions superficials amb relacions d'embolcall moderades rarament necessiten força variable. Les embuticions profundes properes als límits del material, peces amb angles de paret variables o geometries que creen reflujo desigual de la brida s'aprofiten més de la capacitat VBF.

Propietats del material inflen decisivament en la decisió. Els materials amb característiques pronunciades d'enduriment per deformació obtenen un benefici major dels perfils variables. L'acer d'alta resistència, certes aliatges d'alumini i acers inoxidables sovint justifiquen la inversió en VBF només pel comportament del material.

Volum de producció afecta l'economia. La producció de baix volum pot no justificar els costos dels equips VBF llevat que la complexitat de la peça ho requereixi absolutament. Les aplicacions d'alt volum reparteixen la inversió en equipament entre més peces, cosa que fa que el VBF sigui econòmicament atractiu fins i tot per a millores de qualitat moderades.

Taxes actuals de defectes ofereixen orientació pràctica. Si esteu aconseguint una qualitat acceptable amb força constant, el VBF pot oferir rendiments decreixents. Si persisteixen defectes com arrugues o esquinçaments malgrat haver optimitzat els paràmetres de força constant, el VBF sovint proporciona la solució que solament les refinacions de càlcul no poden aconseguir.

Quan avaluïeu sistemes VBF, demaneu dades als proveïdors d'equips que mostrin resultats abans i després d'aplicacions similars a la vostra. La millor evidència prové de millores demostrades en peces comparables, no de capacitats teòriques.

El control de força variable representa l'extrem avançat de l'optimització de la força del premsapeles. Però abans d'implementar estratègies de control sofisticades, necessiteu mètodes fiables per diagnosticar quan els ajustos de força no funcionen com es pretén.

Resolució d'errors habituals de càlcul

El vostre càlcul de la força del premsapeles semblava perfecte sobre el paper. La fórmula era correcta, les dades del material eren precises i els ajustos de la premsa coincidien amb les vostres especificacions. Tanmateix, les peces que surten de la línia expliquen una història diferent: vores arrissades, parets esquerdatades o ratllades misterioses que no haurien d'existir. Què ha anat malament?

Fins i tot els fabricants d'eines i motlles més experimentats es troben en situacions on els valors calculats no es tradueixen en èxit a la producció. L'allunyament entre teoria i realitat sovint es revela mitjançant patrons específics de defectes que apunten directament a problemes amb la força del premsapeles. Aprendre a interpretar aquests patrons us transforma d'algú que reacciona als problemes a algú que els resol sistemàticament.

Diagnòstic dels problemes de arrugament i ruptura

Cada defecte explica una història. Quan examineu una peça defectuosa, la ubicació, el patró i la gravetat del defecte proporcionen pistes diagnòstiques que guien les vostres accions correctores. Un tècnic de matrius qualificat no només veu un rebaix arrugat; veu evidències d'especifics desequilibris de forces que els seus càlculs no havien previst.

L'arrugament indica una restricció insuficient. Quan la força del portamotlles és inferior al llindar necessari per suprimir el pandeig per compressió, el material del rebaix pren el camí de mínima resistència i es corba cap amunt. Observareu patrons ondulats a la zona del rebaix, que de vegades s'estenen fins a la paret quan el material arrugat és estirat cap a la cavitat de la matriu. El límit elàstic de l'acer o d'altres materials estableix la resistència bàsica contra aquest pandeig, però la geometria i les condicions de fricció determinen si la força aplicada supera aquest llindar.

El desgarrament indica una restricció excessiva o un flux de material inadequat. Quan la força del marc d'embolcall crea massa fricció, el punçó continua la seva cursa mentre que la brida no pot alimentar-se prou ràpid. La paret s'estira més enllà dels seus límits de conformació, normalment trencant-se al radi del punçó on les concentracions de tensió són màximes. Les esquerdes poden aparèixer com a petites fissures que es propaguen durant la conformació o com a fractures completes de la paret que separen la copa de la seva brida.

La següent matriu diagnòstica relaciona observacions visuals amb causes probables i accions correctores:

Tipus de defecte	Indicadors visuals	Possible problema de BHF	Acció correctiva
Plecs de brida	Superfície de brida arrugada i ondulada; plecs que es radien des del centre	Força massa baixa; restricció inadequada contra les tensions compressives	Augmentar la pressió específica entre un 15-25%; verificar el contacte uniforme del marc d'embolcall
Plecs de paret	Plecs o ones a la paret de la copa; superfície irregular de la paret	Força severament insuficient; arrugues arrossegades a l'interior de la cavitat	Augmentar significativament la força; comprovar el joc de l'utillatge
Desgarrament al radi del punçó	Grietas o fissures al radi inferior; fractures circumferencials	Força massa elevada; fricció excessiva que restringeix el flux	Redueix la força un 10-20%; millora la lubricació
Fractura de paret	Separació completa de la paret; línies de ruptura esquinçades	Força severament excessiva o material al límit de conformació	Redueix substancialment la força; verifica els límits de la relació d'embutició
Afinament excessiu	Afinament localitzat; reducció visible del gruix a la paret	Força marginalment elevada; deformació propera al límit del diagrama FLD	Redueix la força un 5-15%; millora la lubricació al radi de la matriu
Ratllades superficials	Marques de galling; ratllades paral·leles a la direcció d'estirat	La força pot ser adequada però la fricció localment massa elevada	Inspeccioneu les superfícies del motlle; milloreu la lubricació; polit l'arredoniment del motlle

Observeu com defectes similars poden tenir causes arrel diferents. Un especialista en eines i motlles aprèn a distingir entre problemes relacionats amb la força i altres variables del procés examinant detingudament els patrons de defectes. Les esquerdes circumferencials suggereixen tensió radial deguda a una força excessiva del sujetador de fulla, mentre que les esquerdes longitudinals podrien indicar defectes del material o un joc inadequat del motlle més que problemes de força.

Utilització de mesures per confirmar problemes de força del sujetador de fulla

La inspecció visual us permet començar, però les mesures confirmen el diagnòstic. Dues aproximacions analítiques proporcionen evidència quantitativa que el càlcul de la força del sujetador de fulla necessita ajustos.

Mesures d'espessor revela com es distribueix el material durant l'embutició. Utilitzant un micròmetre esfèric o un mesurador d'espessor ultrasònic, mesureu l'espessor de la paret en diversos punts al voltant de la circumferència del got i a diferents altures. És normal un aprimament uniforme del 10-15%. Un aprimament localitzat superior al 20-25% indica concentracions de deformació que sovint es deuen a problemes amb la força d'aplicació del rib (BHF).

Compareu els perfils d'espessor de peces formades amb diferents ajustos de força. Si l'augment de la força BHF va acompanyat d'un major aprimament al radi del punçó, heu confirmat que la força excessiva n'en és la causa. Si reduir la força BHF elimina l'aprimament però provoca arrugues, heu identificat la vostra finestra de funcionament i cal optimitzar dins aquest rang.

Anàlisi de deformació l'ús de patrons de quadrícula circular o la correlació d'imatges digitals proporciona una visió més profunda. En mesurar com els cercles imprimits es deformen en el·lipses durant el formatejat, podeu representar els camins reals de deformació en un diagrama de límit de formabilitat. Si les deformacions mesurades s'agrupen prop de la zona de arrugament, augmenteu la força. Si s'apropen al límit d'estricció, reduïu la força o corregiu les condicions de fricció.

Quan documenteu defectes per a un fabricant d'utillatges i motlles o per a un equip d'enginyeria, incloeu fotografies amb anotacions de mesures que indiquin exactament on es produeixen els problemes. Aquesta documentació accelera la resolució d'incidències en proporcionar evidències clares en lloc de descripcions subjectives. Comprendre les convencions dels símbols de soldadura no és directament rellevant aquí, però s'aplica el mateix principi de comunicació tècnica clara: una documentació precisa permet solucions precises.

Enfocament sistemàtic per a la resolució de problemes

Quan les peces no superen la inspecció, eviteu la temptació d'ajustar immediatament la força del marc d'embolcall (BHF). Un enfocament sistemàtic assegura que identifiqueu la causa arrel real en lloc d'enmascarar un problema mentre en creeu un altre. Fins i tot una soldadura per solapa que connecta components requereix una seqüència adequada per obtenir resultats de qualitat; la resolució de problemes de BHF exigeix una disciplina similar.

Seguiu aquesta seqüència de resolució de problemes abans d'ajustar la vostra força calculada:

• Verifiqueu les propietats del material: Confirmeu que el material entrant coincideixi amb les especificacions. Comproveu els certificats de farga per a la resistència a la fluència, tolerància de gruix i estat superficial. Les variacions del material entre diferents colades poden desplaçar l'optimal BHF entre un 10-20%.
• Comproveu l'estat de la lubricació: Inspeccioneu la cobertura del lubricant, la viscositat i la contaminació. Una lubricació inadequada o degradada crea variacions de fricció que imiten problemes de BHF. Assegureu-vos que l'aplicació sigui consistent en tota la superfície de la planxa.
• Mesureu el BHF real respecte al calculat: Utilitzeu cèl·lules de càrrega o manòmetres per verificar que la premsa aporti la força programada. La deriva del sistema hidràulic, les fuites del cilindre de nitrogen o el desgast mecànic poden reduir la força real per sota dels valors establerts.
• Inspeccioneu les superfícies de les matrius: Examineu les superfícies del portamatriu i del portablanques en busca de desgast, gripatge o residus. Danys localitzats creen una distribució de pressió irregular que els càlculs suposen uniforme.
• Verifiqueu les dimensions del blanc: Confirmeu que el diàmetre i el gruix del blanc coincideixen amb els valors dissenyats. Els blancs excessivament grans augmenten la superfície de la brida, requerint una força proporcionalment més elevada que la calculada.

Només després de completar aquesta seqüència de verificació hauríeu d'ajustar el vostre càlcul de la força del portablanques. Si el material, lubricació, equip i geometria compleixen correctament amb les especificacions, llavors tornar a calcular amb una pressió específica ajustada esdevé la resposta adequada.

Documenteu cada pas de resolució de problemes i el seu resultat. Aquest registre és inestimable per a futures tirades de producció i ajuda a formar operaris menys experimentats. Un historial de resolució de problemes ben documentat sovint revela patrons: potser el material d’un proveïdor concret necessita sistemàticament una força més elevada del premsapeus, o la humitat estival afecta el rendiment de la lubricació.

Les habilitats de diagnòstic tractades aquí us ajuden a respondre eficaçment quan es produeixen problemes. Però què passaria si poguéssiu predir i prevenir aquests problemes abans de tallar el primer embutit de producció? Aquí és on la validació basada en simulació transforma el vostre enfocament a l’optimització de la força del premsapeus.

Simulació CAE per a la validació de forces

I si pogués comprovar el càlcul de la força del portamotlle abans de tallar una sola planxa d'acer per motlles? La simulació CAE moderna ho fa possible, transformant la manera en què els enginyers validen i ajusten els paràmetres de força. En lloc de confiar únicament en fórmules i proves d'assaig i error, ara podeu visualitzar exactament com fluirà el material, on es produirà l'afilegament i si hi ha riscs d'arrugament al disseny abans de passar a les eines de producció.

L'anàlisi per elements finits (AEF) ha revolucionat l'optimització del conformant profund. Mitjançant la creació de models virtuals de la vostra operació de conformació, el programari de simulació prediu el comportament del material sota diverses condicions de força amb una precisió remarcable. Les propietats que heu estat calculant, com el mòdul d'elasticitat de l'acer i els valors de límit elàstic, es converteixen en entrades que impulsen models matemàtics sofisticats de deformació plàstica. Aquestes simulacions revelen problemes que les fórmules per si soles no poden anticipar, especialment en geometries complexes on les solucions analítiques són insuficients.

Optimització de forces basada en simulació

Penseu en la simulació FEA com un camp d'assaig digital per al vostre càlcul de la força del portamotlles. El programari divideix el vostre motlle, punçó, matriu i portamotlles en milers d'elements petits, i després calcula com es deforma cada element a mesura que el punçó virtual baixa. Les propietats del material, incloent el mòdul d'elasticitat de l'acer, les corbes d'enduriment per deformació i els coeficients d'anisotropia, determinen com respon el metall simulat a les forces aplicades.

El procés de simulació segueix un flux de treball iteratiu. Introduïu el valor de BHF calculat, executeu l'anàlisi i examineu els resultats. Si la peça virtual mostra arrugues a la zona de la brida, augmenteu la força i torneu a executar. Si apareix un aprimament excessiu prop del radi del punçó, reduïu la força o ajusteu els paràmetres de lubricació. Cada iteració triga uns minuts en lloc de les hores necessàries per a les proves físiques, i podeu explorar desenes d'escenaris abans de tallar qualsevol tipus d'acer.

El que fa que les simulacions modernes siguin especialment potents és la seva capacitat per capturar fenòmens que els càlculs manuals només poden aproximar com a màxim. El mòdul elàstic de l'acer afecta com el material recupera la forma després del conformant, i la simulació prediu aquest retroces amb prou precisió per compensar-lo en el disseny del motlle. L'enduriment per deformació canvia les propietats del material durant la cursa, i l'anàlisi per elements finits (FEA) segueix aquests canvis element per element al llarg de tota la seqüència de conformació.

Les sortides de la simulació rellevants per a l'optimització de la força d'embragatge (BHF) inclouen:

• Mapes de distribució del gruix: Visualitzacions codificades per colors que mostren el gruix de la paret en tota la peça, destacant immediatament les zones amb excesiva reducció o augment de gruix
• Prediccions del camí de deformació: Gràfics que mostren com evoluciona l'estat de deformació de cada punt durant el formant, directament comparables amb el diagrama de límit de conformació del vostre material
• Indicadors de risc d'arrugament: Algorismes que detecten inestabilitats compressives abans que es manifestin com a vinclaments visibles, assenyalant les zones que necessiten una major restricció
• Corbes força-desplaçament: Gràfics de la força del punxó i de la força del retenidor de brida al llarg de la cursa, verificant que la vostra premsa té capacitat suficient

Aquestes sortides transformen càlculs abstractes en dades tècniques operatives. Quan una simulació mostra que la vostra FBR calculada produeix un aprimament del 22% al radi del punxó mentre que el límit del material és del 25%, sabeu que teniu un marge acceptable. Quan els indicadors de arrugament s'activen a la brida, sabeu exactament on centrar la vostra atenció.

Del càlcul a l’utillatge preparat per a producció

El camí des de la simulació validada fins als motlles preparats per a producció requereix traduir resultats virtuals a especificacions tècniques físiques. Aquesta traducció exigeix experiència tant en la interpretació de simulacions com en l'enginyeria pràctica de motllos. Una especificació precisa de l'entreferro del motlle en un plànol representa només un detall entre centenars que han de ser executats correctament perquè el motlle funcioni tal com es va simular.

El mòdul de l'acer que introduïu per a la simulació ha de coincidir amb els materials reals de les matrius. Les especificacions d'acabat superficial derivades de les suposicions del coeficient de fricció s'han d'assolir en la fabricació de les matrius. Les toleràncies de planor del portamatriu han de mantenir la distribució uniforme de pressió que heu suposat en la simulació. Tots els detalls estan relacionats amb el fet que la vostra força de pinçament cuidadosament validada produeixi els resultats esperats en producció.

Els equips d'enginyeria que destaquen en aquesta traducció solen integrar la metodologia de càlcul amb la validació de simulacions des de l'inici del projecte. No tracten les fórmules i l'anàlisi per elements finits (FEA) com a activitats separades, sinó com a eines complementàries en un flux de treball unificat. Els càlculs inicials proporcionen punts de partida, les simulacions perfeccionen i validen, i les proves en producció confirmen tota la metodologia.

Empreses com Shaoyi demostra com aquest enfocament integrat proporciona resultats. Les seves avançades capacitats de simulació CAE validen els càlculs de la força del portamotlles durant el desenvolupament del motlle, detectant possibles problemes abans que es fresi l'acer per a eines. Amb la certificació IATF 16949 que assegura els estàndards de gestió de qualitat en tot el procés, la seva metodologia produeix resultats mesurables: una taxa d'aprovació al primer intent del 93%, reflectint que la precisió dels càlculs es trasllada amb èxit a la realitat productiva.

Aquest nivell d'èxit al primer intent no succeeix per atzar. Requereix una validació sistemàtica en cada etapa: calcular la força del portamotlles mitjançant fórmules adequades, simular el flux de material amb dades de propietats precises, ajustar els paràmetres segons els resultats virtuals i fabricar motlles que reprodueixin fidelment les condicions simulades. Quan una geometria específica de retenidor apareix als plànols de disseny del motlle, ha de ser fresada amb precisió, ja que fins i tot detalls aparentment menors afecten el comportament del sistema complet de l'eina.

Per a aplicacions automotrius on les toleràncies dimensionals són estretes i els volums de producció exigeixen una qualitat constant, els càlculs de força del premsatel·les validats per simulació esdevenen essencials. El cost del programari de simulació i del temps d'enginyeria es compensa moltes vegades gràcies a la reducció d'iteracions d'assajos, menys índexs de rebuig i un temps més curt fins a la producció. Les peces que abans necessitaven setmanes d'optimització basada en prova i error ara assolen la qualitat objectiu en pocs dies.

La lliçó pràctica és clara: el vostre càlcul de la força del premsatel·les proporciona la base, però la simulació valida si aquesta base suportarà l'èxit en producció. Juntes, aquestes eines creen una metodologia que transforma el conformant profund d'un art dependent de l'experiència en una disciplina d'enginyeria guiada per dades.

Amb paràmetres de força validats per simulació i eines preparades per a producció, esteu en condicions d'implementar un flux de treball complet de càlcul que integri tots els mètodes tractats en aquesta guia.

Implementació del vostre flux de treball de càlcul

Heu explorat fórmules, efectes de fricció, validació de FLD, sistemes de força variable, mètodes de resolució de problemes i capacitats de simulació. Ara és el moment d'ajuntar-ho tot en un flux de treball coherent que pugueu aplicar de manera consistent en diferents projectes. La diferència entre els enginyers que tenen dificultats amb l'estampat profund i aquells que aconsegueixen resultats fiables sovint es deu a una metodologia sistemàtica més que a la capacitat de càlcul pura.

Un enfocament estructurat assegura que no ometeu passos clau quan les pressions del termini us obliguen a avançar ràpidament. També genera documentació que accelera els treballs futurs i ajuda a formar membres de l'equip en pràctiques provades. Sigui que esteu calculant la força per a una copa cilíndrica senzilla o per a un panell automobilístic complex, s'aplica el mateix flux de treball fonamental amb ajustos adequats segons la complexitat.

Selecció de l'enfocament de càlcul adequat

Abans de començar amb els càlculs, heu de seleccionar la metodologia que s'ajusti als requisits de la vostra aplicació. No tots els treballs justifiquen el mateix nivell de rigor analític. Una execució ràpida de prototipus de cinquanta peces exigeix un enfocament diferent del llançament d'un programa de producció anual d'un milió d'unitats. Comprendre els compromisos entre els mètodes us ajuda a assignar eficaçment els recursos d'enginyeria.

Hi ha tres enfocaments principals per al càlcul de la força del retenidor de fulla, cadascun amb característiques distintes que s'adapten a diferents escenaris. L'equació per trobar la resistència a la fluència al 0,2 per cent a partir de dades tensió-deformació il·lustra el nivell de caracterització del material que requereix cada mètode. Les fórmules empíriques simples funcionen amb valors de resistència a la fluència de taules tècniques, mentre que els mètodes analítics avançats poden necessitar corbes de flux completes que mostrin el comportament dels acers a la fluència durant la deformació plàstica.

Criteris	Fórmules empíriques	Mètodes analítics	Enfocaments basats en FLD
Nivell d'exactitud	±15-25% típic	±10-15% amb bones dades	±5-10% amb FLD validat
Requisits de dades	Bàsic: límit elàstic, gruix, geometria	Moderat: propietats completes del material, coeficients de fricció	Amples: corbes completes de FLD, mesures de deformació
Complexitat	Baix; càlculs manuals suficients	Moderat; full de càlcul o programari de càlcul	Alt; requereix simulació o anàlisi física de deformació
Escenaris d'ús òptim	Peça simples axialsimètriques, estimacions inicials, proves de prototips	Components de producció, complexitat moderada, materials establerts	Aplicacions crítiques, materials nous, toleràncies estretes
Temps d'enginyeria	Minuts a hores	Hores a dies	Dies a setmanes
S'esperen iteracions d'intent	3-5 ajustos típics	1-3 ajustos típics	Sovent èxit a la primera passada

Comprendre què significa el límit elàstic en la pràctica us ajuda a interpretar aquests rangs de precisió. Les comparacions entre el límit elàstic i la resistència a la tracció mostren que el límit elàstic representa l'esforç a partir del qual comença la deformació permanent, convertint-lo en el paràmetre clau per als càlculs de BHF. Si les dades del vostre material només inclouen la resistència a la tracció, hauréu d'estimar el límit elàstic, introduint una incertesa que els mètodes empírics ja tenen en compte, però amb la qual els mètodes analítics costa corregir.

Per a la majoria d'aplicacions de producció, els mètodes analítics assolen el punt òptim entre esforç i precisió. Es dedica prou temps d'enginyeria per assolir resultats fiables sense necessitat de les proves extensives que exigeix la validació basada en FLD. Reservi els mètodes FLD per a aplicacions en què el cost dels defectes justifiqui una anàlisi exhaustiva inicial: components crítics de seguretat, programes d’alta volumetria on millores petites es multipliquen al llarg de milions de peces, o materials nous sense directrius establertes per al formant.

Construcció del flux de treball per al càlcul de BHF

Independentment de l'enfocament de càlcul que trii, el següent flux de treball assegura una cobertura completa de tots els factors que influeixen en la força del portaplomes. Consideri aquesta seqüència com la seva llista de comprovació de qualitat: completar cada pas de manera sistemàtica evita errors que poden causar problemes en producció.

1. Recopilar dades del material i especificacions geomètriques: Recopileu totes les dades abans de començar els càlculs. Això inclou el diàmetre en blanc, el diàmetre del punxó, el radi de la cantonada de la matriu, el gruix del material i totes les dades completes de les propietats del material. Verifiqueu amb quins valors de límit elàstic esteu treballant: dades de certificació de laminat, estimacions de manuals o proves de tracció reals. Confirmeu que les unitats siguin consistents en tota la documentació. Les dades mancants o inexactes condeneu els càlculs des del principi.
2. Calculeu la FMB inicial mitjançant la fórmula adequada: Apliqueu la fórmula estàndard FMB = π/4 × [(D₀² - (d + 2rd)²)] × p amb la pressió específica apropiada per al material. Per a geometries complexes, considereu un preanàlisi per elements finits. Documenteu totes les hipòtesis, especialment pel que fa a la selecció de la pressió específica. Aquest valor calculat es converteix en la base per a totes les refinacions posteriors.
3. Ajusteu segons les condicions de fricció i lubricació: Modifiqueu la vostra BHF de base segons les condicions reals del taller. Si utilitzeu compostos de trefilat pesats amb coeficients de fricció d'uns 0,05-0,08, el valor calculat probablement sigui vàlid. Amb lubricació més lleugera o materials sense recobriment, pot ser necessari un augment de força del 15-30%. Documenteu quin lubricant esteu assumint perquè el personal de producció pugui mantenir aquestes condicions.
4. Valideu segons les restriccions de FLD: Per a aplicacions crítiques, verifiqueu que els vostres ajustos de força mantinguin les trajectòries de deformació del material dins dels límits segurs d'embutició. Si teniu accés a simulació, feu assaigs virtuals i representeu gràficament les deformacions predites respecte a la FLD del vostre material. Si confieu en l'experiència, compareu la vostra geometria i combinació de materials amb treballs similars exitosos. Assenyaleu qualsevol condició en què s'estiguin apropant als límits coneguts.
5. Verifiqueu mitjançant simulació o assaigs experimentals: Abans del compromís de producció, confirmeu els vostres càlculs amb evidències físiques. La simulació proporciona verificació virtual; les proves reals amb peces proporcionen la confirmació definitiva. Mesureu les distribucions d'espessor, reviseu si hi ha arrugues o reducció d'espessor i ajusteu els paràmetres de força segons sigui necessari. Documenteu quins ajustos van ser necessaris i per què.
6. Documenteu i estandaritzeu per a la producció: Creeu especificacions de producció que recullin els paràmetres validats de BHF juntament amb totes les condicions que s'han de mantenir: tipus de lubricant i mètode d'aplicació, requisits d'especificació del material, intervals de manteniment del motlle i criteris d'inspecció. Aquesta documentació assegura una qualitat consistent entre torns i operadors.

Consideració clau: La documentació creada en el pas sis es converteix en el punt de partida per a treballs futurs similars. Amb el temps, construireu una base de coneixement de paràmetres validats que accelerarà la enginyeria de noves peces mentre redueix l'incertesa dels càlculs.

Connectar l'excel·lència en el càlcul amb l'èxit en la producció

Seguir aquest procés de treball transforma sistemàticament el càlcul de la força del portamatriu d'una tasca d'enginyeria aïllada en una base per a l'èxit manufacturador. La disciplina de recopilar dades completes, calcular amb rigor, validar resultats i documentar resultats genera beneficis acumulatius a tot arreu de la vostra operació.

Considereu com la comprensió de la resistència a la fluència respecte a la resistència a la tracció flueix a través d'aquest procés de treball. Dades precises del material al pas u permeten càlculs precisos al pas dos. Aquests càlculs prediuen requisits de força realistes al pas tres. La validació als passos quatre i cinc confirma que les vostres suposicions sobre el material coincidien amb la realitat. La documentació al pas sis captura aquest coneixement validat per a ús futur. Cada pas es basa en els passos anteriors, i tota la cadena només és tan forta com el seu eslabó més feble.

Per a organitzacions que busquen accelerar aquest procés de treball sense sacrificar qualitat, les col·laboracions amb especialistes en motlles d'estampació de precisió poden reduir dràsticament els terminis. Shaoyi exemplifica aquest enfocament, oferint prototipatge ràpid en tan sols 5 dies mantenint alhora la validació rigorosa que exigeix l'èxit en producció. Les seves capacitats de fabricació d’alta volumetria amb eines econòmiques adaptades als estàndards dels OEM demostren com la metodologia adequada de càlcul de BHF es tradueix directament en matrius d'estampació automotriu preparades per a producció.

Tant si esteu calculant la força per al vostre proper projecte com si esteu avaluant socis que puguin donar suport a les vostres operacions d’estampació, els principis romanen invariables. Els càlculs precisos comencen entenent què significa realment la resistència a la fluència i les propietats del material per a la vostra aplicació específica. La validació sistemàtica assegura que els valors calculats funcionin en la realitat de la producció. I la documentació exhaustiva preserva el coneixement que fa que cada projecte posterior sigui més eficient.

El càlcul de la força del portablanques no consisteix només a prevenir arrugues en peces individuals. Es tracta de desenvolupar la disciplina d'enginyeria i la infraestructura de coneixement que permeten una qualitat constant al llarg de milers o milions de cicles de producció. Domineu aquest procés, i descobrireu que els reptes del conformant profund es converteixen en problemes d'enginyeria gestionables, en lloc de fonts frustrants de rebuts i retrabalts.

Preguntes freqüents sobre el càlcul de la força del portablanques

1. Què és la força del portablanques?

La força del portablanques (BHF) és la pressió de sujecció aplicada a la zona de brida d'un embutit de xapa metàl·lica durant operacions de conformant profund. Controla el flux de material des de la brida cap a la cavitat de la matriu, evitant arrugues causades per tensions compressives i alhora evitant una fricció excessiva que pugui provocar ruptures. La BHF òptima equilibra aquests dos modes de fallada contraposats per produir peces sense defectes i amb un gruix de paret uniforme.

2. Quina és la fórmula per al càlcul de la força del portablanques?

La fórmula estàndard és BHF = π/4 × [(D₀² - (d + 2rd)²)] × p, on D₀ és el diàmetre de la planxa, d és el diàmetre del punzó, rd és el radi de la cantonada de la matriu i p és la pressió específica del retenidor en MPa. El terme entre claudàtors calcula l'àrea anular de la brida sota el retenidor, que després es multiplica per valors de pressió específics del material que varien entre 1-4 MPa segons si s'està conformant alumini, acer o acer inoxidable.

3. Com es calcula la força d'estirat?

La força d'estirat utilitza la fórmula F_draw = C × t × S, on C és la circumferència mitjana del diàmetre del cos, t és el gruix del material i S és la resistència a la tracció del material. La força del retenidor de planxa sol variar entre el 30-40% de la força màxima del punzó. Ambdós càlculs funcionen conjuntament: la BHF controla la restricció del material mentre que la força d'estirat supera la fricció i la resistència del material per arrossegar la planxa cap a la cavitat de la matriu.

4. Com afecta la fricció als càlculs de la força del retenidor de planxa?

La fricció amplia l'efecte de restricció de qualsevol força de premsatelles (BHF) mitjançant la relació Força d'embutició = BHF × μ × e^(μθ), on μ és el coeficient de fricció i θ és l'angle d'envoltura. Els coeficients típics varien entre 0,03-0,05 per a pel·lícules polimèriques i 0,15-0,20 per al contacte acer sobre acer sec. Una fricció més elevada significa que es necessita una BHF més baixa per assolir la mateixa restricció, mentre que una lubricació inadequada pot requerir un augment de força del 15-30%.

5. Quan hauria d'utilitzar una força de premsatelles variable en lloc d'una força constant?

La força de premsatelles variable (VBF) té un rendiment superior al de la força constant en embuticions profundes properes als límits del material, geometries complexes asimètriques i materials amb altes taxes d'enduriment per deformació. Els sistemes VBF comencen amb una força més elevada per evitar arrugues inicials quan l'àrea de la brida és més gran, i després redueixen la pressió a mesura que la brida disminueix. Això elimina el compromís inherent en els mètodes de força constant, permetent assolir geometries impossibles amb ajustos estàtics.